









«ј ќЌ» «ќ“ќ√ќ ѕ≈–≈“»Ќ”
Ћюдина розр≥зн¤Ї предмети що њњ оточуютьт за формою. ÷≥кав≥сть до форми ¤кого-небудь предмета може бути продиктована життЇвою необх≥дн≥стю, а може бути викликана красою форми. ‘орма, в основ≥ побудови ¤коњ лежать комб≥нац≥¤ симетр≥њ й золотого перетину, спри¤Ї найкращому зоровому сприйн¤ттю та по¤в≥ в≥дчутт¤ краси й гармон≥њ. ÷≥ле завжди складаЇтьс¤ ≥з частин, частини р≥зноњ величини перебувають у певному в≥дношенн≥ одна до одноњ та до ц≥лого. ѕринцип золотого перетину – вищий про¤в структурноњ ≥ функц≥ональноњ досконалост≥ ц≥лого ≥ його частин у мистецтв≥, науц≥, техн≥ц≥, природ≥.
«олотий перетин – гармон≥йна пропорц≥¤
” математиц≥ пропорц≥Їю (лат. proportio) називають р≥вн≥сть двох в≥дносин: a : b = c : d.
¬≥др≥зок пр¤моњ ј¬ можна розд≥лити на дв≥ частини такими способами:
• на дв≥ р≥вн≥ частини – ј¬ : ј— = ј¬ : ¬—;
• на дв≥ нер≥вн≥ частини в будь-¤кому в≥дношенн≥ (так≥ частини пропорц≥њ не утворюють);
• таким чином, коли ј¬ : ј— = ј— : ¬—.
ќстаннЇ ≥ Ї золотий розпод≥л або розпод≥л в≥др≥зка в крайньому й середньому в≥дношенн≥.
«олотий перетин – цей такий пропорц≥йний розпод≥л в≥др≥зка на нер≥вн≥ частини, при ¤кому увесь в≥др≥зок так в≥дноситьс¤ до б≥льшоњ частини, ¤к б≥льша частина в≥дноситьс¤ до меншоњ; або ≥накше кажучи, менший в≥др≥зок так ставитьс¤ до б≥льшого, ¤к б≥льший до всього
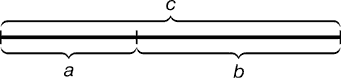
a : b = b : c або с : b = b : а.
–ис. 1. √еометричне зображенн¤ золотоњ пропорц≥њ
ѕрактичне знайомство ≥з золотим перетином починають ≥з розпод≥лу в≥др≥зка пр¤моњ у золот≥й пропорц≥њ за допомогою циркул¤ та л≥н≥йки.
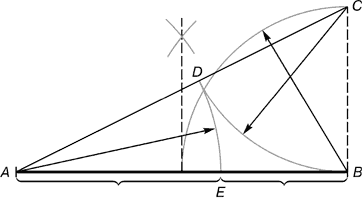
–ис. 2. –озпод≥л в≥др≥зка пр¤м≥й по золотому перетину. BC = 1/2 AB; CD = BC
≤з точки ¬ вибудовуЇтьс¤ перпендикул¤р, що дор≥внюЇ половин≥ ј¬. ќтримана точка — з´ЇднуЇтьс¤ л≥н≥Їю ≥з точкою ј. Ќа отриман≥й л≥н≥њ в≥дкладаЇтьс¤ в≥др≥зок ¬—, що зак≥нчуЇтьс¤ точкою D. ¬≥др≥зок AD переноситьс¤ на пр¤му ј¬. ќтримана при цьому точка ≈ д≥лить в≥др≥зок ј¬ у сп≥вв≥дношенн≥ золотоњ пропорц≥њ.
¬≥др≥зки золотоњ пропорц≥њ виражаютьс¤ неск≥нченним ≥ррац≥ональним дробом AE = 0,618..., ¤кщо ј¬ прийн¤ти за одиницю, ¬≈ = 0,382... ƒл¤ практичних ц≥лей часто використовують наближен≥ значенн¤ 0,62 ≥ 0,38. якщо в≥др≥зок ј¬ прийн¤ти за 100 частин, то б≥льша частина в≥др≥зка р≥вна 62, а менша – 38 частинам.
¬ластивост≥ золотого перетину описуютьс¤ р≥вн¤нн¤м:
x2 – x – 1 = 0.
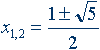
–≥шенн¤ цього р≥вн¤нн¤:
¬ластивост≥ золотого перетину створили навколо цього числа романтичний ореол таЇмничост≥ й ледве чине м≥стичного поклон≥нн¤.
ƒругий золотий перетин
Ѕолгарський журнал "Ѕатьк≥вщина" (є10, 1983 р.) опубл≥кував статтю ÷ветана ÷екова- ќл≥вц¤ "ѕ–ќ другий золотий перетин", ¤ке випливаЇ з основного перетину й даЇ ≥нше в≥дношенн¤ 44:56 .
“ака пропорц≥¤ ви¤влена в арх≥тектур≥, а також маЇ м≥сце при побудов≥ композиц≥й зображень подовженого горизонтального формату.
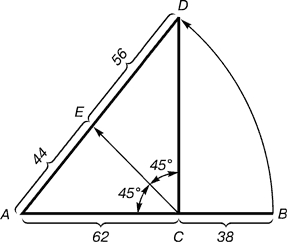
–ис. 3. ѕобудова другого золотого перетину
–озпод≥л зд≥йснюЇтьс¤ в такий спос≥б. ¬≥др≥зок ј¬ д≥литьс¤ в пропорц≥њ золотого перетину. ≤з крапки — проводитьс¤ перпендикул¤р —D. –ад≥ус ј¬ перетинаЇ CD перетин утворюЇ точку D, ¤ка з´ ЇднуЇтьс¤ л≥н≥Їю ≥з точкою ј. ѕр¤мий кут ј—D д≥литьс¤ навп≥л. ≤з точки — проводитьс¤ л≥н≥¤ до перетину з л≥н≥Їю AD. “очка ≈ д≥лить в≥др≥зок AD у в≥дношенн≥ 56:44.
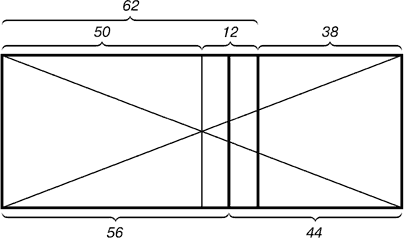
–ис. 4. –озпод≥л пр¤мокутника л≥н≥Їю другого золотого перетину
Ќа малюнку показане положенн¤ л≥н≥њ другого золотого перетину. ¬она перебуваЇ посередин≥ м≥ж л≥н≥Їю золотого перетину й середньою л≥н≥Їю пр¤мокутника.
«олотий трикутник
ƒл¤ знаходженн¤ в≥др≥зк≥в золотоњ пропорц≥њ висх≥дного й спадного р¤д≥в можна користуватис¤ пентаграмою.
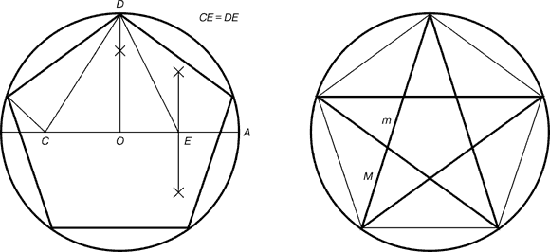
–ис. 5. ѕобудова правильного п´ ¤тикутника й пентаграми
ƒл¤ побудови пентаграми необх≥дно побудувати правильний п´ ¤тикутник. —пос≥б його побудови розробив н≥мецький живописець ≥ граф≥к јльбрехт ƒюрер (1471...1528). Ќехай O – центр окружност≥, A – точка на окружност≥ та ≈ – середина в≥др≥зка ќј. ѕерпендикул¤р до рад≥уса ќј, вставлений у точц≥ ќ, перетинаЇтьс¤ з окружн≥стю в точц≥ D. ористуючись циркулем, в≥дкладемо на д≥аметр≥ в≥др≥зок CE = ED. ƒовжина сторони вписаного в окружн≥сть правильного п´ ¤тикутника р≥вна DC. ¬≥дкладаЇмо на окружност≥ в≥др≥зки DC ≥ одержимо п´ ¤ть крапок дл¤ накресленн¤ правильного п´ ¤тикутника. «´ ЇднуЇмо кути п´ ¤тикутника через один д≥агонал¤ми й одержуЇмо пентаграмою. ”с≥ д≥агонал≥ п´ ¤тикутника д≥л¤ть один одного на в≥др≥зки, зв´ ¤зан≥ м≥ж собою золотою пропорц≥Їю.
ожний к≥нець п’¤ти кутноњ з≥рки ¤вл¤Ї собою золотий трикутник. …ого сторони утворюють кут 36° при вершин≥, а п≥дстава, в≥дкладене на б≥чну сторону, д≥лить њњ в пропорц≥њ золотого перетину.
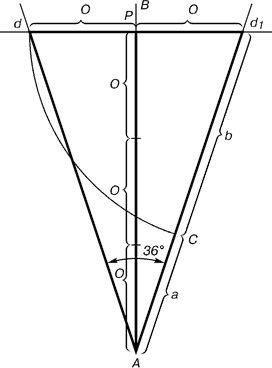
–ис. 6. ѕобудова золотого трикутника
ѕроводимо пр¤му ј¬. ¬≥д крапки ј в≥дкладаЇмо на н≥й три рази в≥др≥зок ќ дов≥льноњ величини, через отриману точку – проводимо перпендикул¤р до л≥н≥њ ј¬, на перпендикул¤р≥ вправо й ул≥во в≥д точки – в≥дкладаЇмо в≥др≥зки ќ. ќтриман≥ крапки d ≥ d1 з´ ЇднуЇмо пр¤мими ≥з крапкою ј. ¬≥др≥зок dd1 в≥дкладаЇмо на л≥н≥ю Ad1, одержуючи крапку —. ¬она розд≥лила л≥н≥ю Ad1 у пропорц≥њ золотого перетину. Ћ≥н≥¤ми Ad1 ≥ dd1 користуютьс¤ дл¤ побудови "золотого" пр¤мокутника.
≤стор≥¤ золотого перетину
ѕрийн¤то вважати, що пон¤тт¤ про золотий розпод≥л ув≥в у науковий побут ѕ≥фагор, давньогрецький ф≥лософ ≥ математик (VI в. до н.е.). ™ припущенн¤, що ѕ≥фагор своЇ знанн¤ золотого розпод≥лу запозичив у Їгипт¤н ≥ жител≥в вав≥лону. ≤ д≥йсно, пропорц≥њ п≥рам≥ди ’еопса, храм≥в, барельЇф≥в, предмет≥в побуту та прикрас ≥з гробниц≥ “утанхамона св≥дчать, що Їгипетськ≥ майстри користувалис¤ сп≥вв≥дношенн¤ми золотого розпод≥лу при њхньому створенн≥. ‘ранцузький арх≥тектор Ће орбюзье знайшов, що в рельЇф≥ ≥з храму фараона ћереж≥ I в јбидосе й у рельЇф≥, що зображуЇ фараона –амзеса, пропорц≥њ ф≥гур в≥дпов≥дають величинам золотого розпод≥лу. «одчий ’есира, зображений на рельЇф≥ дерев´ ¤ноњ дошки ≥з гробниц≥ його ≥мен≥, тримаЇ в руках вим≥рювальн≥ ≥нструменти, у ¤ких заф≥ксован≥ пропорц≥њ золотого розпод≥лу.
√реки були митецькими геометрами. Ќав≥ть арифметиц≥ навчали своњх д≥тей за допомогою геометричних ф≥гур. вадрат ѕ≥фагора й д≥агональ цього квадрата були основою дл¤ побудови динам≥чних пр¤мокутник≥в.
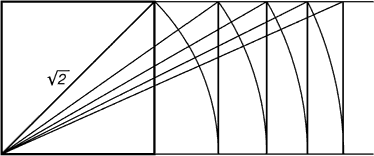
–ис. 7. ƒинам≥чн≥ пр¤мокутники
ѕлатон (427...347 рр. до н.е.) також знав про золотий розпод≥л. …ого д≥алог "“имейимей, “име" присв¤чений математичним ≥ естетичним погл¤дам школи ѕ≥фагора ≥, зокрема , питанн¤м золотого розпод≥лу.
Ќа фасад≥ давньогрецького храму ѕарфенона присутн≥ золот≥ пропорц≥њ. ѕри його розкопках ви¤влен≥ циркул≥, ¤кими користувалис¤ арх≥тектори й скульптори античного миру. ” ѕомпейскому циркул≥ (музей у Ќеапол≥) також закладен≥ пропорц≥њ золотого розпод≥лу.
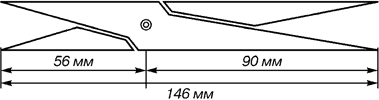
–ис. 8. јнтичний циркуль золотого перетину
¬ античн≥й л≥тератур≥ золотий розпод≥л уперше згадуЇтьс¤ в "ѕочатках" ≈вкл≥да. ¬ 2- й книз≥ "ѕочав" даЇтьс¤ геометрична побудова золотого розпод≥лу ѕ≥сл¤ ≈вкл≥да досл≥дженн¤м золотого розпод≥лу займалис¤ √ипсикл (II в. до н.е.), ѕапп (III в. н.е.) ≥ ≥н. ” середньов≥чн≥й ™вроп≥ ≥з золотим розпод≥лом познайомилис¤ по арабських перекладах "ѕочав" ≈вкл≥да. ѕерекладач ƒж. ампано з Ќаварри (III в.) зробив до перекладу коментар≥. —екрети золотого розпод≥лу ревно обер≥галис¤, збер≥галис¤ в строг≥й таЇмниц≥. ¬они були в≥дом≥ т≥льки присв¤ченим.
¬ епоху ¬≥дродженн¤ п≥дсилюЇтьс¤ ≥нтерес до золотого розпод≥лу серед учених ≥ художник≥в у зв´¤зку з його застосуванн¤м ¤к у геометр≥њ, так ≥ в мистецтв≥, особливо в арх≥тектур≥ Ћеонардо да ¬≥нч≥, художник ≥ вчений, бачив, що в ≥тал≥йських художник≥в емп≥ричний досв≥д великий, а знань мало. ¬≥н задумав ≥ початк≥в писати книгу з геометр≥њ, але в цей час з´¤вилас¤ книга ченц¤ Ћуки ѕачол≥, ≥ Ћеонардо залишив свою вит≥вку. Ќа думку сучасник≥в ≥ ≥сторик≥в науки, Ћука ѕачол≥ був справжн≥м св≥тилом, найб≥льшим математиком ≤тал≥њ в пер≥од м≥ж ‘≥боначч≥ й √алилеем. Ћука ѕачол≥ був учнем художника ѕьеро делла ‘ранчески, що написав дв≥ книги, одна з ¤ких називалас¤ "ѕ–ќ перспективу в живопис≥". …ого вважають творцем нарисноњ геометр≥њ.
Ћука ѕачол≥ прекрасно розум≥в значенн¤ науки дл¤ мистецтва. ¬ 1496 р. за запрошенн¤м герцога ћоро в≥н прињжджаЇ в ћ≥лан, де читаЇ лекц≥њ по математиц≥. ” ћ≥лан≥ при двор≥ ћоро в той час працював ≥ Ћеонардо ƒа ¬≥нч≥. ¬ 1509 р. у ¬енец≥њ була видана книга Ћуки ѕачол≥ "Ѕожественна пропорц≥¤" ≥з блискуче виконаними ≥люстрац≥¤ми, через що починають, що њх зробив Ћеонардо ƒа ¬≥нч≥. нига була захопленим г≥мном золотоњ пропорц≥њ. —еред багатьох г≥дностей золотоњ пропорц≥њ чернець Ћука ѕачол≥ не проминув назвати ≥ њњ "божественну суть" ¤к вираженн¤ божественноњ триЇдност≥ бог син, бог батько й бог дух св¤тий (малос¤ на уваз≥, що малий в≥др≥зок Ї уособленн¤ бога сина, б≥льший в≥др≥зок – бога батька, а весь в≥др≥зок – бога духу св¤того).
Ћеонардо ƒа ¬≥нч≥ також багато уваги прид≥л¤в вивченню золотого розпод≥лу. ¬≥н робив перетини стереометричного т≥ла, утвореного правильними п´ ¤тикутниками, ≥ щораз одержував пр¤мокутники з в≥дносинами стор≥н у золотому розпод≥л≥. “ому в≥н дав цьому розпод≥лу назва золота перетин. “ак воно й тримаЇтьс¤ дотепер ¤к найпопул¤рн≥ше.
” той же час на п≥вноч≥ ™вропи, у Ќ≥меччин≥, над тими ж проблемами працював јльбрехт ƒюрер. ¬≥н робить начерки введенн¤ до першого вар≥анта трактату про пропорц≥њ. ƒюрер пише. "Ќеобх≥дно, щоб той, хто що-небудь ум≥Ї, навчив цьому ≥нших, ¤к≥ в цьому б≥дують. ÷е ¤ й нам≥ривс¤ зробити".
—уд¤чи з лист≥в ƒюрера, в≥н зустр≥чавс¤ з Ћукою ѕачоли п≥д час перебуванн¤ в ≤тал≥њ. јльбрехт ƒюрер докладно розробл¤Ї теор≥ю пропорц≥й людського т≥ла. ¬ажливе м≥сце у своњй систем≥ сп≥вв≥дношень ƒюрер в≥дводив золотому перетину. –≥ст людини д≥литьс¤ в золотих пропорц≥¤х л≥н≥Їю по¤са, а також л≥н≥Їю, проведеноњ через к≥нчики середн≥х пальц≥в опущених рук, нижн¤ частина особи – ротом ≥ т.д. ¬≥домий пропорц≥йний циркуль ƒюрера.
¬еликий астроном XVI в. »оган еплер назвав золотий перетин одним з≥ скарб≥в геометр≥њ. ¬≥н перший звертаЇ увагу на значенн¤ золотоњ пропорц≥њ дл¤ ботан≥ки (р≥ст рослин ≥ њх будова).
еплер називав золоту пропорц≥ю, що продовжуЇ саму себе "”лаштована вона так, – писав в≥н, – що два молодш≥ члени ц≥Їњ неск≥нченноњ пропорц≥њ в сум≥ дають трет≥й член, а будь-¤к≥ два останн≥ члени, ¤кщо њх скласти, дають наступний член, причому та ж пропорц≥¤ збер≥гаЇтьс¤ неск≥нченно ".
ѕобудова р¤ду в≥др≥зк≥в золотоњ пропорц≥њ можна робити ¤к уб≥к зб≥льшенн¤ (зростаючий р¤д), так ≥ уб≥к зменшенн¤ (спадний р¤д).
якщо на пр¤моњ дов≥льноњ довжини, в≥дкласти в≥др≥зок m, поруч в≥дкладаЇмо в≥др≥зок M. Ќа п≥дстав≥ цих двох в≥др≥зк≥в вишиковуЇмо шкалу в≥др≥зк≥в золотоњ пропорц≥њ висх≥дного й спадного р¤д≥в
![]()
–ис. 9. ѕобудова шкали в≥др≥зк≥в золотоњ пропорц≥њ
” наступн≥ стол≥тт¤ правило золотоњ пропорц≥њ перетворилос¤ в академ≥чний канон ≥, коли згодом у мистецтв≥ почалас¤ боротьба з академ≥чною рутиною, у запал≥ боротьби "разом з водою виплеснули й дитину". «нову "в≥дкрите" золотий перетин був у середин≥ XIX ст. ¬ 1855 р. н≥мецький досл≥дник золотого перетину професор ÷ейз≥нг опубл≥кував свою працю "≈стетичн≥ досл≥дженн¤". ≤з ÷ейз≥нгом в≥дбулос¤ саме те, що й повинне було неминуче в≥дбутис¤ з досл≥дником, ¤кий розгл¤даЇ ¤вище ¤к таке, без зв´¤зку з ≥ншими ¤вищами. ¬≥н абсолютизував пропорц≥ю золотого перетину, оголосивши њњ ун≥версальноњ дл¤ вс≥х ¤вищ природи й мистецтва. ” ÷ейз≥нга були численн≥ посл≥довники, але були й супротивники, ¤к≥ оголосили його вченн¤ про пропорц≥њ "математичною естетикою".
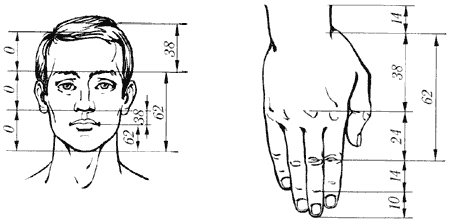
–ис. 10. «олот≥ пропорц≥њ в частинах т≥ла людину
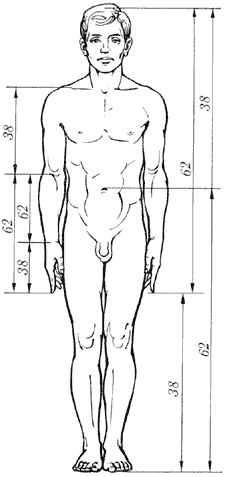
–ис. 11. «олот≥ пропорц≥њ у ф≥гур≥ людини
÷ейз≥нг проробив колосальну роботу. ¬≥н вим≥р¤в близько двох тис¤ч людських т≥л ≥ д≥йшов висновку, що золотий перетин виражаЇ середн≥й статистичний закон. –озпод≥л т≥ла точкою пупа – найважлив≥ший показник золотого перетину. ѕропорц≥њ чолов≥чого т≥ла коливаютьс¤ в межах середнього в≥дношенн¤ 13:8 = 1,625 ≥ трохи ближче п≥дход¤ть уводити, увести до ладу золотому перетину, чому пропорц≥њ ж≥ночого т≥ла, у в≥дношенн≥ ¤кого середнЇ значенн¤ пропорц≥њ виражаЇтьс¤ в сп≥вв≥дношенн≥ 8:5 = 1,6. ” немовл¤ти пропорц≥¤ становить в≥дношенн¤ 1:1 , до 13 рок≥в вона р≥вна 1,6, а до 21 року р≥вн¤Їтьс¤ чолов≥чий. ѕропорц≥њ золотого перетину про¤вл¤ютьс¤ й у в≥дношенн≥ ≥нших частин т≥ла – довжина плеча, передпл≥чч¤ й кист≥, кист≥ й пальц≥в ≥ т.≥н.
—праведлив≥сть своЇњ теор≥њ ÷ейз≥нг перев≥р¤в на грецьких стату¤х. Ќайб≥льше докладно в≥н розробив пропорц≥њ јполлона Ѕельведерського. ѕ≥ддалис¤ досл≥дженню грецьк≥ вази, арх≥тектурн≥ спорудженн¤ р≥зних епох, рослини, тварини, пташин≥ ¤йц¤, музичн≥ тони, в≥ршован≥ розм≥ри. ÷ейз≥нг дав визначенн¤ золотому перетину, показав, ¤к воно виражаЇтьс¤ у в≥др≥зках пр¤моњ й у цифрах. оли цифри, що виражають довжини в≥др≥зк≥в, були отриман≥, ÷ейз≥нг побачив, що вони становл¤ть р¤д ‘≥боначчи, ¤кий можна продовжувати неск≥нченно в одну й в ≥ншу сторону. Ќаступна його книга мала назву "«олотий розпод≥л ¤к основний морфолог≥чний закон у природ≥ й мистецтв≥". ¬ 1876 г. у –ос≥њ була видана невелика книжка, майже брошура, з викладом ц≥Їњ прац≥ ÷ейзинга. јвтор укривс¤ п≥д ≥н≥ц≥алами ё.‘.¬. ” цьому виданн≥ не згаданий жодний здобуток живопису.
Ќјѕ–» ≤Ќ÷≤ XIX – початку XX ст. з´ ¤вилос¤ чимало чисто формал≥стичних теор≥й, про застосуванн¤ золотого перетину у творах мистецтва й арх≥тектури. « розвитком дизайну й техн≥чноњ естетики чинн≥сть закону золотого перетину поширилас¤ на конструюванн¤ машин, мебл≥в ≥ т.≥н.
–¤д ‘≥боначчи
« ≥стор≥Їю золотого перетину непр¤мим образом зв´ ¤зане ≥м´ ¤ ≥тал≥йського математика ченц¤ Ћеонардо з ѕ≥зи, б≥льш в≥домого п≥д ≥менем ‘≥боначчи (син Ѕоначчи). ¬≥н багато подорожував по —ход≥, познайомив ™вропу з ≥нд≥йськими (арабськими) цифрами. ¬ 1202 г вийшов у св≥т його математична прац¤ " нига про абак" (рахунков≥й дошц≥), у ¤к≥м були з≥бран≥ вс≥ в≥дом≥ на той час завданн¤. ќдна ≥з завдань говорила "—к≥льки пар кролик≥в в один р≥к в≥д одн≥Їњ пари народитьс¤".
ћ≥ркуючи на цю тему, ‘ибоначчи вибудував такий р¤д цифр:

–¤д чисел 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55 ≥ т.≥н. в≥домий ¤к р¤д ‘≥боначчи. ќсоблив≥сть посл≥довност≥ чисел пол¤гаЇ в тому, що кожний њњ член, починаючи ≥з третього, дор≥внюЇ сум≥ двох попередн≥х 2 + 3 = 5; 3 + 5 = 8; 5 + 8 = 13, 8 + 13 = 21; 13 + 21 = 34 ≥ т.д., а в≥дношенн¤ сум≥жних чисел р¤ду наближаЇтьс¤ до в≥дношенн¤ золотого розпод≥лу. “ак, 21:34 = 0,617, а 34:55 = 0,618. ÷е в≥дношенн¤ позначаЇтьс¤ символом ‘.
“≥льки це в≥дношенн¤ – 0,618 : 0,382 – даЇ безперервний розпод≥л в≥др≥зка пр¤м≥й у золотоњ пропорц≥њ, зб≥льшенн¤ його або зменшенн¤ неск≥нченно , коли менший в≥др≥зок так ставитьс¤ до б≥льшого, ¤к б≥льший до всього.
‘≥боначчи так само займавс¤ р≥шенн¤м практичних потреб торг≥вл≥: за допомогою ¤коњ найменшоњ к≥лькост≥ гир можна зважити товар? ‘≥боначчи доводить, що оптимальною Ї така система гир: 1, 2, 4, 8, 16...
”загальнений золотий перетин
–¤д ‘≥боначчи м≥г би залишитис¤ т≥льки математичним казусом, ¤кби не та обставина, що вс≥ досл≥дники золотого розпод≥лу в рослинному й у тваринному св≥т≥, не говор¤чи вже про мистецтво, незм≥нно приходили до цього р¤ду ¤к арифметичного вираженн¤ закону золотого розпод≥лу.
”чен≥ продовжували активно розбудовувати теор≥ю чисел ‘≥боначчи й золотого перетину. ё. ћати¤сев≥ч ≥з використанн¤м чисел ‘≥боначчи вир≥шуЇ 10-у проблему √≥лберта. ¬иникають витончен≥ методи р≥шенн¤ р¤ду к≥бернетичних завдань (теор≥њ пошуку, ≥гор, програмуванн¤) з використанн¤м чисел ‘≥боначчи й золотого перетину. ” —Ўј створюЇтьс¤ нав≥ть ћатематична ‘≥боначчи- јсоц≥ац≥¤, ¤ка з 1963 року випускаЇ спец≥альний журнал.
ќдним з дос¤гнень у ц≥й област≥ Ї в≥дкритт¤ узагальнених чисел ‘≥боначчи й узагальнених золотих перетин≥в.
–¤д ‘≥боначчи (1, 1, 2, 3, 5, 8) ≥ в≥дкритий њм же "дв≥йковий" р¤д гир 1, 2, 4, 8, 16... на перший погл¤д зовс≥м р≥зн≥. јле алгоритми њх побудови досить схож≥ один на одного: у першому випадку кожне число Ї сума попереднього числа ≥з самим собою 2 = 1 + 1; 4 = 2 + 2..., у другому – це сума двох попередн≥х чисел 2 = 1 + 1, 3 = 2 + 1, 5 = 3 + 2.... чи неможна в≥дшукати загальну математичну формулу, з ¤коњ виход¤ть ≥ "дв≥йковий" р¤д, ≥ р¤д ‘≥боначчи? ј може бути, ц¤ формула дасть нам нов≥ числов≥ безл≥ч≥, що волод≥ють ¤кимись новими ун≥кальними властивост¤ми?
ƒ≥йсно, задамос¤ числовим параметром S, ¤кий може ухвалювати будь-¤к≥ значенн¤: 0, 1, 2, 3, 4, 5... –озгл¤немо числовий р¤д, S + 1 перших член≥в ¤кого – одиниц≥, а кожний з наступних дор≥внюЇ сум≥ двох член≥в попереднього й в≥ддаленого в≥д попереднього на S крок≥в. якщо n- й член цього р¤ду ми позначимо через ?S (n), то одержимо загальну формулу ?S (n) = ?S (n – 1) + ?S (n – S – 1).
ќчевидно, що при S = 0 ≥з ц≥Їњ формули ми одержимо "дв≥йковий" р¤д, при S = 1 – р¤д ‘≥боначчи, при S = 2, 3, 4. нов≥ р¤ди чисел, ¤к≥ одержали назву S- „исел ‘≥боначчи.
” загальному вид≥ золота S- ѕропорц≥¤ Ї позитивний кор≥нь р≥вн¤нн¤ золотого S- ѕеретину xs+1 – xs – 1 = 0.
Ќеважко показати, що при S = 0 виходить розпод≥л в≥др≥зка навп≥л, а при S = 1 – знайомий класичний золотий перетин.
¬≥дносини сус≥дн≥х S- „исел ‘≥боначчи з абсолютною математичною точн≥стю зб≥гаютьс¤ в меж≥ ≥з золотими S- ѕропорц≥¤ми! ћатематики в таких випадках говор¤ть, що золот≥ S- ѕеретини Ї числовими ≥нвар≥антами S- „исел ‘≥боначчи.
‘акти, що п≥дтверджують ≥снуванн¤ золотих S- ѕеретин≥в у природ≥, приводить б≥лоруський учений ™.ћ. —ороко в книз≥ "—труктурна гармон≥¤ систем" (ћ≥нськ, "Ќаука й техн≥ка", 1984). ¬и¤вл¤Їтьс¤, наприклад, що добре вивчен≥ подв≥йн≥ сплави мають особлив≥, ¤скраво вираженими функц≥ональними властивост¤ми (ст≥йк≥ в терм≥чн≥м в≥дношенн≥, тверд≥, зносост≥йк≥, ст≥йк≥ до окисленн¤ й т.≥н.) т≥льки в тому випадку, ¤кщо питом≥ ваги вих≥дних компонент≥в зв´¤зано один з одним одн≥Їю ≥з золотих S- ѕропорц≥й. ÷е дозволило автору висунути г≥потезу про те, що золотий S- перетин Ї числовий ≥нвар≥ант систем, що будуть п≥дтверджен≥ експериментально, ц¤ г≥потеза мала фундаментальне значенн¤ дл¤ розвитку синергетики – нова галузь науки, що вивчала процес ≥ у самоорган≥зац≥йних системах.
«а допомогою код≥в золотий S- пропорц≥њ можна виразити будь-¤ке д≥йсне число у вигл¤д≥ суми ступен≥в золотих S- пропорц≥й ≥з ц≥лими коеф≥ц≥Їнтами.
ѕринципова в≥дм≥нн≥сть такого способу кодуванн¤ чисел пол¤гаЇ в тому, що п≥дстави нових код≥в, що представл¤ють собою золот≥ S- ѕропорц≥њ, при S > 0 ви¤вл¤ютьс¤ ≥ррац≥ональними числами. “аким чином, нов≥ системи численн¤ з ≥ррац≥ональними п≥дставами ¤к би ставл¤ть "з голови на ноги" ≥сторично складену ≥Їрарх≥ю в≥дносин м≥ж числами рац≥ональними й ≥ррац≥ональними. —права в тому, що спочатку були "в≥дкрит≥" числа натуральн≥; пот≥м њх в≥дносини – числа рац≥ональн≥. ≤ лише п≥зн≥ше – п≥сл¤ в≥дкритт¤ п≥фагор≥йц¤ми непор≥вн¤нних в≥др≥зк≥в – на св≥тло з´¤вилис¤ ≥ррац≥ональн≥ числа. —кажемо, у дес¤тков≥й, п’¤тер≥чноњ, дв≥йковоњ й ≥нших класичних позиц≥йних системах численн¤ ¤к своЇр≥дноњ першооснови були обран≥ натуральн≥ числа – 10, 5, 2, – з ¤ких уже за певними правилами конструювалис¤ вс≥ ≥нш≥ натуральн≥, а також рац≥ональн≥ й ≥ррац≥ональн≥ числа.
—вого роду альтернативою ≥снуючим способам численн¤ виступаЇ нова, ≥ррац≥ональна система, у ¤кост≥ першооснови, початку численн¤ ¤коњ обрано ≥ррац≥ональне число (що Ї, нагадаЇмо, коренем р≥вн¤нн¤ золотого перетину); через нього вже виражаютьс¤ ≥нш≥ д≥йсн≥ числа.
” так≥й систем≥ численн¤ будь-¤ке натуральне число завжди у¤вимо у вигл¤д≥ к≥нцевоњ – а не неск≥нченноњ, ¤к думали ран≥ше! – суми ступен≥в кожноњ ≥з золотих S- ѕропорц≥й. ÷е одна ≥з причин, чому "≥ррац≥ональна" арифметика, волод≥ючи дивною математичною простотою й доб≥рн≥стю, ¤к би ув≥брала в себе кращ≥ ¤кост≥ класичноњ дв≥йковоњ й "‘≥боначчиЇвоњ" арифметик.
ѕринципи формоутворенн¤ в природ≥
”се, що здобувало ¤кусь форму, утворювалос¤, росло, прагнуло зайн¤ти м≥сце в простор≥ й зберегти себе. ÷е прагненн¤ знаходить зд≥йсненн¤ в основному у двох вар≥антах – р≥ст нагору або розстел¤нн¤ по поверхн≥ земл≥ й закручуванн¤ по сп≥рал≥.
–аковина закручена по сп≥рал≥. якщо њњ розгорнути, то виходить довжина, що небагато уступаЇ довжин≥ зм≥њ. Ќевелика дес¤ти сантиметрова раковина маЇ сп≥раль довжиною 35 див. —пирал≥ дуже поширен≥ в природ≥. ¬истава про золотий перетин буде неповним, ¤кщо не сказати про сп≥раль.
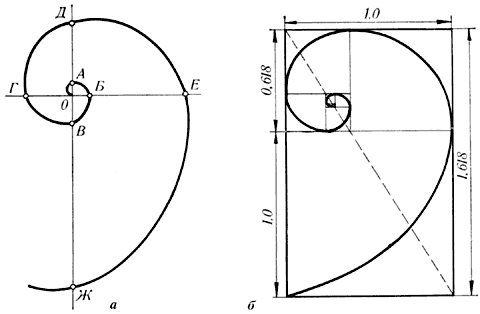
–ис. 12. —п≥раль јрх≥меда
‘орма сп≥рально завитоњ раковини привернула увагу јрх≥меда. ¬≥н вивчав њњ й вив≥в р≥вн¤нн¤ сп≥рал≥. —п≥раль, накреслена по цьому р≥вн¤нню, називаЇтьс¤ його ≥менем. «б≥льшенн¤ њњ кроку завжди р≥вном≥рно. ” цей час сп≥раль јрх≥меда широко застосовуЇтьс¤ в техн≥ку.
ўе •ете п≥дкреслював тенденц≥ю природи до сп≥ральност≥. √винтопод≥бне й сп≥ральне розташуванн¤ лист≥в на г≥лках дерев пом≥тили давно. —п≥раль побачили в розташуванн≥ нас≥нн¤ сон¤шника, у шишках сосни, ананасах, кактусах ≥ т.д. —п≥льна робота ботан≥к≥в ≥ математик≥в пролила св≥тло на ц≥ дивн≥ ¤вища природи. «´¤сувалос¤, що в розташуванн≥ лист≥в на г≥лц≥ (ф≥лотаксис), нас≥нн¤ сон¤шника, шишок сосни про¤вл¤Ї себе р¤д ‘≥боначчи, а стало бути, про¤вл¤Ї себе закон золотого перетину. ѕавук плете павутину сп≥ралепод≥бно. —п≥раллю закручуЇтьс¤ бурев≥й. ѕерел¤кана череда п≥вн≥чних олен≥в розб≥гаЇтьс¤ по сп≥рал≥. ћолекула ƒЌ закручена подв≥йною сп≥раллю. •ете називав сп≥раль "кривого житт¤".
—еред пришл¤хових трав росте н≥чим не прим≥тна рослина – цикор≥й. ѕридивимос¤ до нього уважно. ¬≥д основного стебла утворювавс¤ в≥дросток. ¬≥дразу розташувавс¤ перший листок.
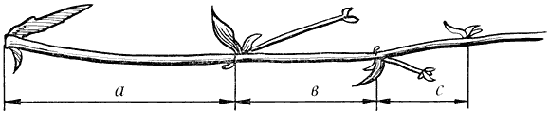
–ис. 13. ÷икор≥й
¬≥дросток робить сильний викид у прост≥р, зупин¤Їтьс¤, випускаЇ листок, але вже коротше першого, знову робить викид у прост≥р, але вже меншоњ сили, випускаЇ листок ще меншого розм≥ру й знову викид. якщо перший викид прийн¤ти за 100 одиниць, то другий р≥вний 62 одиниц¤м, трет≥й – 38, четвертий – 24 ≥ т.д. ƒовжина пелюстк≥в теж п≥длегла золотоњ пропорц≥њ. ” росту, завоюванн≥ простору рослина збер≥гала певн≥ пропорц≥њ. ≤мпульси його росту поступово зменшувалис¤ в пропорц≥њ золотого перетину.
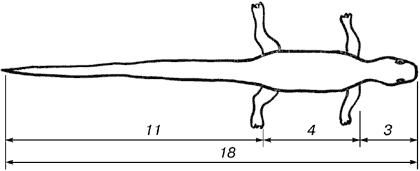
–ис. 14. ящ≥рка живородна
” ¤щ≥рц≥ з першого погл¤ду вловлюютьс¤ приЇмн≥ дл¤ нашого ока пропорц≥њ – довжина њњ хвоста так ставитьс¤ до довжини ≥ншого т≥ла, ¤к 62 до 38.
≤ в рослинному, ≥ у тваринному св≥т≥ наполегливо пробиваЇтьс¤ формотворна тенденц≥¤ природи – симетр≥¤ щодо напр¤мку росту й руху. “ут золотий перетин про¤вл¤Їтьс¤ в пропорц≥¤х частин перпендикул¤рно до напр¤мку росту.
ѕрирода зд≥йснила розпод≥л на симетричн≥ частини й золот≥ пропорц≥њ. ” частинах про¤вл¤Їтьс¤ повторенн¤ будови ц≥лого.
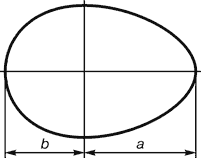
–ис. 15. яйце птаха
¬еликий •ете, поет, натурал≥ст ≥ художник (в≥н малював ≥ писав аквареллю), мр≥¤в про створенн¤ Їдиного вченн¤ про форму, утв≥р ≥ перетворенн≥ орган≥чних тел. ÷е в≥н ув≥в у науковий побут терм≥н морфолог≥¤.
ѕер юр≥ на початку нашого стор≥чч¤ сформулював р¤д глибоких ≥дей симетр≥њ. ¬≥н затверджував, що не можна розгл¤дати симетр≥ю ¤кого-небудь т≥ла, не враховуючи симетр≥ю навколишнього середовища.
«аконом≥рност≥ "золотий" симетр≥њ про¤вл¤ютьс¤ в енергетичних переходах елементарних часток, у будов≥ де¤ких х≥м≥чних сполук, у планетарних ≥ косм≥чних системах, у генних структурах живих орган≥зм≥в. ÷≥ законом≥рност≥, ¤к зазначено вище, Ї в будов≥ окремих орган≥в людини й т≥ла в ц≥лому, а також про¤вл¤ютьс¤ в б≥оритмах ≥ функц≥онуванн≥ головного мозку й зорового сприйн¤тт¤.
«олотий перетин ≥ симетр≥¤
«олотий перетин не можна розгл¤дати саме по соб≥, окремо, без зв´¤зку ≥з симетр≥Їю. ¬еликий рос≥¤нин кристалограф √.¬.¬ульф (1863...1925) вважав золотий перетин одним ≥з про¤в≥в симетр≥њ.
«олотий розпод≥л не Ї про¤в асиметр≥њ, чогось протилежного симетр≥њ «г≥дно ≥з сучасними виставами золотий розпод≥л – це асиметрична симетр≥¤. ¬ науку про симетр≥ю ув≥йшли так≥ пон¤тт¤, ¤к статична й динам≥чна симетр≥¤. —татична симетр≥¤ характеризуЇ спок≥й, р≥вновагу, а динам≥чна – рух, р≥ст. “ак, у природ≥ статична симетр≥¤ представлена будовою кристал≥в, а в мистецтв≥ характеризуЇ спок≥й, р≥вновагу й нерухом≥сть. ƒинам≥чна симетр≥¤ виражаЇ активн≥сть, характеризуЇ рух, розвиток, ритм, вона – св≥дченн¤ житт¤. —татичноњ симетр≥њ властив≥ р≥вн≥ в≥др≥зки, р≥вн≥ величини. ƒинам≥чн≥й симетр≥њ властиве зб≥льшенн¤ в≥др≥зк≥в або њх зменшенн¤, ≥ воно виражаЇтьс¤ у величинах золотого перетину зростаючого або убутного р¤ду.



